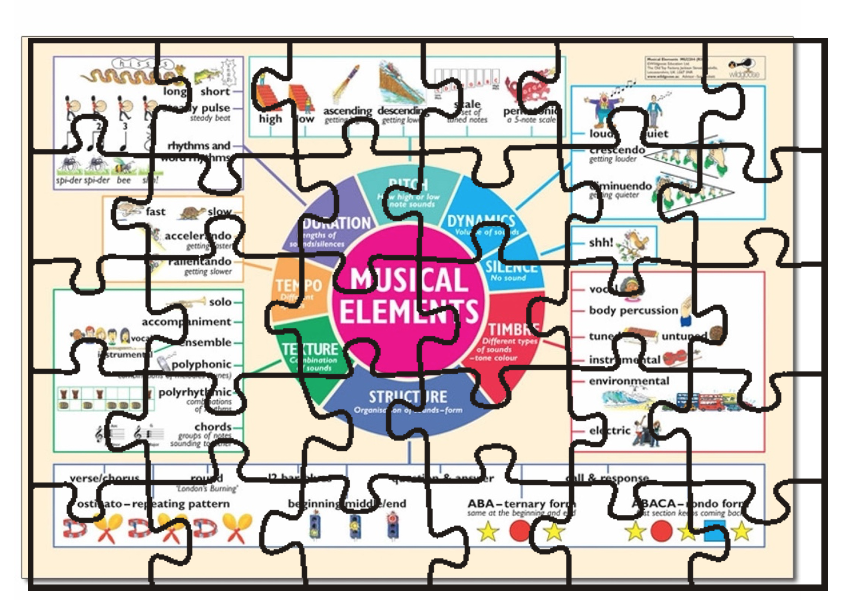
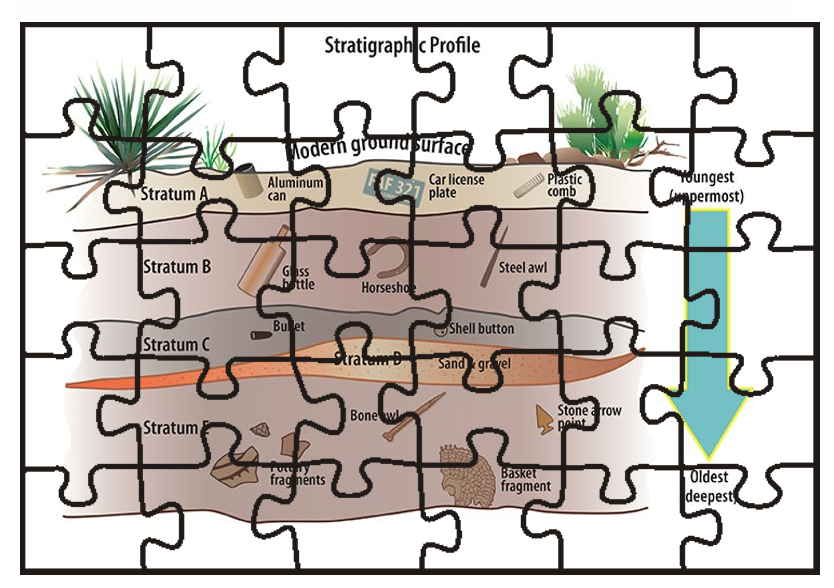
You caught a beauty!!!
Download PDF of scaffold here.
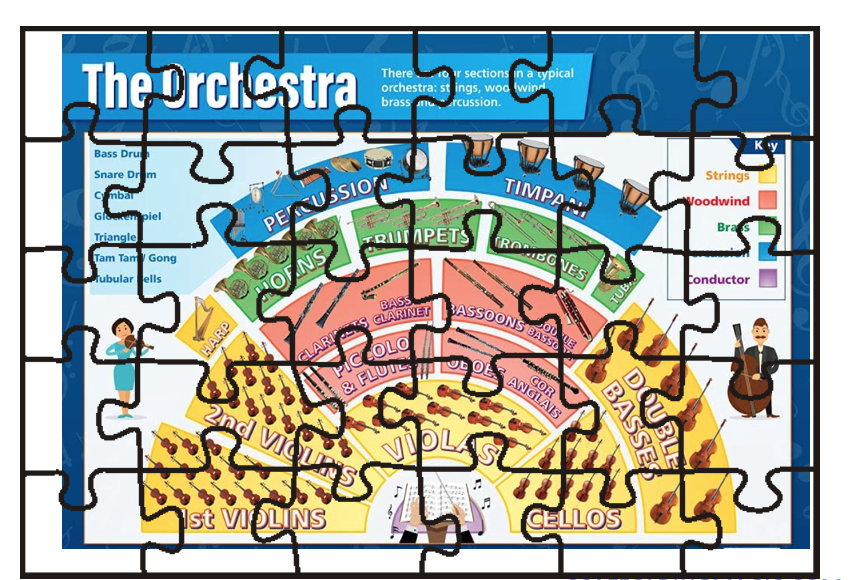
Download PDF of scaffold here.
theory behind the scaffold…
One of the greatest challenges we have as teachers is to present new information that doesn’t create cognitive overload. Many times, we ask our students to learn a large amount of information that is difficult for them to assimilate – either because of the content, an incompatible learning style, or because of insufficient time for them to work on it thoroughly.
In these circumstances, mental resources become stretched and the ability to assimilate the required material is reduced.* Experts affirm that we can learn no more than seven (7) elements at a time. If you think about how much information our students are exposed to daily, we’d be more compassionate in what we demand of them in our lessons and possibly introduce new knowledge in more varied ways so as to honour the learning styles of a larger percent of them.
Using interactive scaffolding techniques such as puzzles helps to reduce the stress on mental resources by creating a problem-solving activity that combines multi-sensory foci. The action of putting them together calls on many different learning styles. Aside from being entertaining, puzzles create opportunities for students to practice motor and cognitive skills that might otherwise be ignored after the first years of Primary school.
The beneficial part of this particular type of puzzle is that they can be used for any subject. You’ll see below how teachers of mathematics, history, art, music, science, can all take advantage of the same template, to engage their students and let them learn autonomously. You’ll see how easy it is to adapt the activity to your needs.
Step by step…
- Choose a puzzle template that has repetitive pattern pieces (the objective being for your students to solve the puzzle based on the information placed in the puzzle and not by the shape of the pieces.)
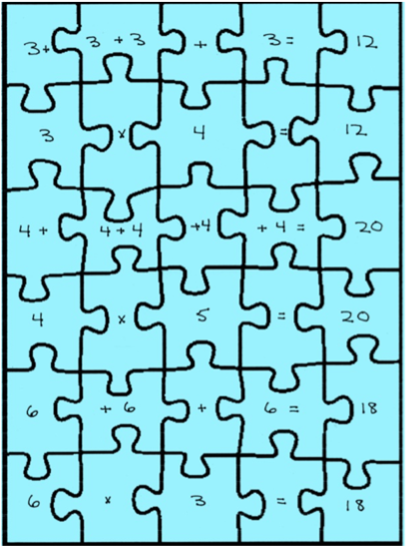
2. Write or type the information onto the puzzle template. (In the example below, a mathematics teacher has created a puzzle that presents addition and multiplication. As students put the puzzle together, they might slowly understand that multiplication is simply a shortcut of adding numbers together.*)
- Make one copy of the puzzle for each pair of students
- Cut them up, and hand them out. (You’ll see in the video explanation of the scaffold, cutting the puzzles is much easier than you may think. If you print out the information on different colours of paper, you can cut up to six at a time, so that you can separate them easily afterwards, and so reducing the bulk of your work.)
- Note: Speak as little as possible before students begin the activity. Write out instructions and avoid giving away the core of the puzzle (which is, in this case, the correlation between adding and multiplication).
Scaffolding activities are meant to override the need for verbal explanation of new information until after the students have interacted with it first. The goal is that they work with new knowledge through varied learning styles and in this way, they can practice critical thinking. By working on their own, first, you are giving them time to assimilate elements at their own pace and in different ways. Later, if you need to explain parts of the information verbally, they will have a stronger basis upon which they can construct the new concepts.
- Prepare questions on the information in the puzzle. In this way, those pairs/groups who finish before others have a meaningful extension to do while the others are finishing. In some cases, you might even include the questions in the puzzle itself.
- Formative Assessment:
- Give groups different addition problems than appeared in the puzzle. They come up with corresponding multiplication equations.
- Ask groups to summarise/conclude/paraphrase the information.
- Reflection: Students write 75-100 words on the dynamic of the activity and how it felt to come up with the concept of multiplication by themselves instead of through direct teaching.
* One of the challenges of teaching mathematics is to evaluate how much direct instruction to give students versus how to support them at a distance as they engage in self-learning. We need to trust that students can gain knowledge by themselves through problem-solving activities – on their own or in groups. We can facilitate strategies that they can use, but learning goes much deeper when they arrive at explanations and answers without being directed and/or told explicitly what the answers are.
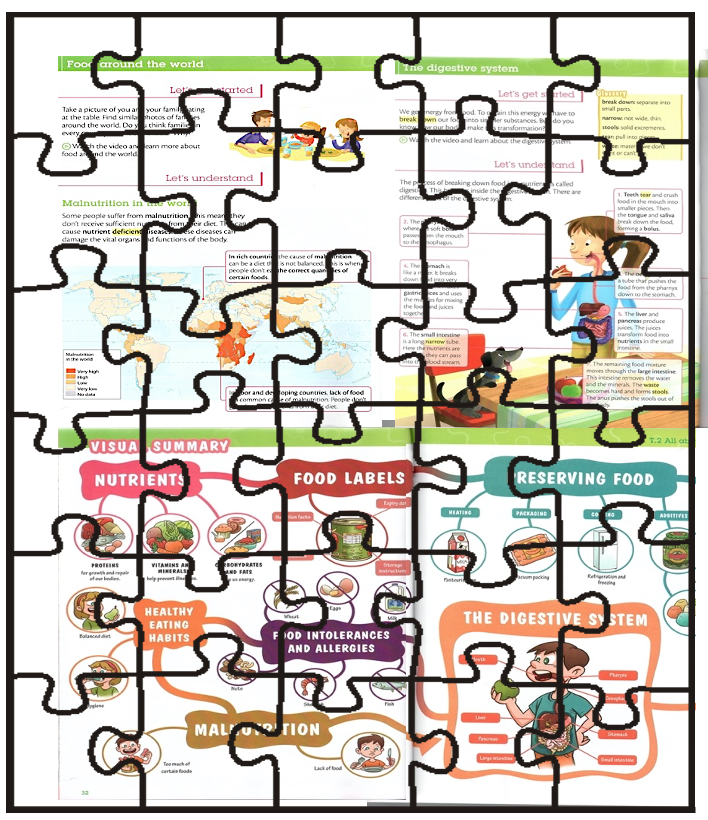
Other examples of puzzles as scaffolds In these cases, you print out copies of the information on different coloured paper, one copy of the template. Then, place six copies of the information under one template and in this way you can cut six at a time.
video explanation of scaffold…
* Hattie, John (2015). Visible Learning and the Science of How We Learn. Routledge Press.

Scaffoldingmagic.com is your entryway into DYNAMIC bilingual learning methodologies, such as Phenomenon-Based Learning, CLIL, EMI, and ESL. You’ll find ways to implement critical thinking tools (DOK) to promote higher level thinking, the growth mindset, instill an ethic of excellence, deep reflection on learning, and all through multi-cultural, interdisciplinary activities. We have the keys to turning competences into action and to creating collective efficacy in your school so you move ahead as a unified, enthusiastic team.